Retractions and inverse Retractions
The exponential and logarithmic map might be too expensive to evaluate or not be available in a very stable numerical way on certain manifolds $\mathcal M$. Retractions provide a possibly cheap, fast and stable alternative.
A retraction $\operatorname{retr}_p: T_p\mathcal M → \mathcal M$ is a smooth map that fulfils (for all $p∈\mathcal M$) that
- $\operatorname{retr}_p(0) = p$
- $D\operatorname{retr}_p(0): T_p\mathcal M \to T_p\mathcal M$ is the identity map,
i.e. $D\operatorname{retr}_p(0)[X]=X$ holds for all $X∈ T_p\mathcal M$,
where $D\operatorname{retr}_p$ denotes the differential of the retraction.
A retraction $\operatorname{retr}_p$ can be interpreted as a first order approximation to the exponential map $\exp_p$.
The retraction is called of second order if for all $X$ the curves $c(t) = R_p(tX)$ have a zero acceleration at $t=0$, i.e. $c''(0) = 0$.
The following figure compares the exponential map exp(M, p, X) on the Circle (ℂ) (or Sphere(1) embedded in $ℝ^2$) with one possible retraction, the one based on projections. Note especially that $\operatorname{dist}(p,q)=\lVert X\rVert_p$ while this is not the case for the result $\operatorname{retr}_p(X) = q'$.
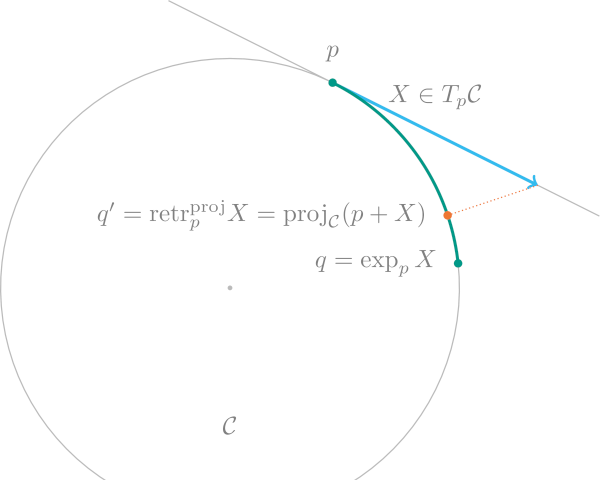
Similar to the exponential map the retraction might not be globally invertible, but locally it is. So locally one can define the inverse retraction $\operatorname{retr}_p^{-1}\colon \mathcal M \to T_p\mathcal M$, which can be seen as a first order approximation to the logarithmic map. Within the ManifoldsBase.jl interface the inverse retraction is called inverse_retract.
The general interface looks as follows.
ManifoldsBase.default_inverse_retraction_method — Method
default_inverse_retraction_method(M::AbstractManifold)
default_inverse_retraction_method(M::AbstractManifold, ::Type{T}) where {T}The AbstractInverseRetractionMethod that is used when calling inverse_retract without specifying the inverse retraction method. By default, this is the LogarithmicInverseRetraction.
This method can also be specified more precisely with a point type T, for the case that on a M there are two different representations of points, which provide different inverse retraction methods.
ManifoldsBase.default_inverse_retraction_method — Method
default_inverse_retraction_method(M::AbstractManifold)
default_inverse_retraction_method(M::AbstractManifold, ::Type{T}) where {T}The AbstractInverseRetractionMethod that is used when calling inverse_retract without specifying the inverse retraction method. By default, this is the LogarithmicInverseRetraction.
This method can also be specified more precisely with a point type T, for the case that on a M there are two different representations of points, which provide different inverse retraction methods.
ManifoldsBase.default_retraction_method — Method
default_retraction_method(M::AbstractManifold)
default_retraction_method(M::AbstractManifold, ::Type{T}) where {T}The AbstractRetractionMethod that is used when calling retract without specifying the retraction method. By default, this is the ExponentialRetraction.
This method can also be specified more precisely with a point type T, for the case that on a M there are two different representations of points, which provide different retraction methods.
ManifoldsBase.default_retraction_method — Method
default_retraction_method(M::AbstractManifold)
default_retraction_method(M::AbstractManifold, ::Type{T}) where {T}The AbstractRetractionMethod that is used when calling retract without specifying the retraction method. By default, this is the ExponentialRetraction.
This method can also be specified more precisely with a point type T, for the case that on a M there are two different representations of points, which provide different retraction methods.
ManifoldsBase.inverse_retract — Function
inverse_retract(M::AbstractManifold, p, q)
inverse_retract(M::AbstractManifold, p, q, method::AbstractInverseRetractionMethod)Compute the inverse retraction, a cheaper, approximate version of the logarithmic map, of points p and q on the AbstractManifold M.
Inverse retraction method can be specified by the last argument, defaulting to default_inverse_retraction_method(M, typeof(p)). For available inverse retractions on certain manifolds see the documentation on the corresponding manifold.
See also retract.
ManifoldsBase.inverse_retract! — Function
inverse_retract!(M::AbstractManifold, X, p, q[, method::AbstractInverseRetractionMethod])Compute the inverse retraction, a cheaper, approximate version of the logarithmic map, of points p and q on the AbstractManifold M. Result is saved to X.
Inverse retraction method can be specified by the last argument, defaulting to default_inverse_retraction_method(M, typeof(p)). See the documentation of respective manifolds for available methods.
See also retract!.
ManifoldsBase.retract — Function
retract(M::AbstractManifold, p, X, method::AbstractRetractionMethod=default_retraction_method(M, typeof(p)))
retract!(M::AbstractManifold, q, p, X, method::AbstractRetractionMethod=default_retraction_method(M, typeof(p)))Compute a retraction, an approximate version of the exponential map, from p into direction X on the AbstractManifold M. This can be computed in-place of q.
A retraction $\operatorname{retr}_p: T_p\mathcal M → \mathcal M$ is a smooth map that fulfils
- $\operatorname{retr}_p(0) = p$
- $D\operatorname{retr}_p(0): T_p\mathcal M → T_p\mathcal M$ is the identity map,
i.e. $D\operatorname{retr}_p(0)[X]=X$ holds for all $X∈ T_p\mathcal M$,
where $D\operatorname{retr}_p$ denotes the differential of the retraction
The retraction is called of second order if for all $X$ the curves $c(t) = \operatorname{retr}_p(tX)$ have a zero acceleration at $t=0$, i.e. $c''(0) = 0$.
Retraction method can be specified by the last argument, defaulting to default_retraction_method(M, typeof(p)). For further available retractions see the documentation of respective manifolds.
Locally, the retraction is invertible. For the inverse operation, see inverse_retract.
ManifoldsBase.retract! — Function
retract(M::AbstractManifold, p, X, method::AbstractRetractionMethod=default_retraction_method(M, typeof(p)))
retract!(M::AbstractManifold, q, p, X, method::AbstractRetractionMethod=default_retraction_method(M, typeof(p)))Compute a retraction, an approximate version of the exponential map, from p into direction X on the AbstractManifold M. This can be computed in-place of q.
A retraction $\operatorname{retr}_p: T_p\mathcal M → \mathcal M$ is a smooth map that fulfils
- $\operatorname{retr}_p(0) = p$
- $D\operatorname{retr}_p(0): T_p\mathcal M → T_p\mathcal M$ is the identity map,
i.e. $D\operatorname{retr}_p(0)[X]=X$ holds for all $X∈ T_p\mathcal M$,
where $D\operatorname{retr}_p$ denotes the differential of the retraction
The retraction is called of second order if for all $X$ the curves $c(t) = \operatorname{retr}_p(tX)$ have a zero acceleration at $t=0$, i.e. $c''(0) = 0$.
Retraction method can be specified by the last argument, defaulting to default_retraction_method(M, typeof(p)). For further available retractions see the documentation of respective manifolds.
Locally, the retraction is invertible. For the inverse operation, see inverse_retract.
Types of Retractions
To distinguish different types of retractions, the last argument of the retraction as well as its inverse specifies a type. The following ones are available.
ManifoldsBase.AbstractInverseRetractionMethod — Type
AbstractInverseRetractionMethod <: AbstractApproximationMethodAbstract type for methods for inverting a retraction (see inverse_retract).
ManifoldsBase.AbstractRetractionMethod — Type
AbstractRetractionMethod <: AbstractApproximationMethodAbstract type for methods for retracting a tangent vector to a manifold.
ManifoldsBase.ApproximateExponentialRetraction — Type
ApproximateExponentialRetraction{N <: NamedTuple} <: ApproximateRetractionRetraction using an algorithm with certain parameters to approximate the exponential map.
The intended implementation should use solve_chart_exp_ode.
Fields
keyword_arguments– a named tuple containing the parameters meant to be the keywords for the approximation algorithm
Constructor
ApproximateExponentialRetraction(keyword_arguments::NamedTuple)ManifoldsBase.ApproximateInverseRetraction — Type
ApproximateInverseRetraction <: AbstractInverseRetractionMethodAn abstract type for representing approximate inverse retraction methods.
ManifoldsBase.ApproximateLogarithmicInverseRetraction — Type
ApproximateLogarithmicInverseRetraction{N <: NamedTuple} <: ApproximateInverseRetractionInverse retraction using an algorithm with certain parameters to approximate the logarithmic map.
The intended implementation should use solve_chart_log_bvp.
Fields
keyword_arguments– a named tuple containing the parameters meant to be the keywords for the approximation algorithm
Constructor
ApproximateLogarithmicInverseRetraction(keyword_arguments::NamedTuple)ManifoldsBase.ApproximateRetraction — Type
ApproximateRetraction <: AbstractRetractionMethodAn abstract type for representing approximate retraction methods.
ManifoldsBase.CayleyInverseRetraction — Type
CayleyInverseRetraction <: AbstractInverseRetractionMethodAn inverse retraction based on the Cayley transform, which is realized by using the PadeInverseRetraction{1}.
Though you would call e.g. inverse_retract(M, p, q, CayleyInverseRetraction()), to implement an inverse Cayley retraction, define inverse_retract_cayley!(M, X, p, q) for your manifold M. By default both these functions fall back to calling a PadeInverseRetraction(1).
ManifoldsBase.CayleyRetraction — Type
CayleyRetraction <: AbstractRetractionMethodA retraction based on the Cayley transform, which is realized by using the PadeRetraction{1}.
Though you would call e.g. retract(M, p, X, CayleyRetraction()), to implement a Cayley retraction, define retract_cayley!(M, q, p, X; kwargs...) for your manifold M. By default both these functions fall back to calling a PadeRetraction(1), whose fused variant retract_pade_fused!(M, q, p, X, t, m; kwargs...), which retracts t*X without forming that product, can additionally be implemented for performance reasons.
ManifoldsBase.EmbeddedInverseRetraction — Type
EmbeddedInverseRetraction{T<:AbstractInverseRetractionMethod} <: AbstractInverseRetractionMethodCompute an inverse retraction by using the inverse retraction of type T in the embedding and projecting the result
Constructor
EmbeddedInverseRetraction(r::AbstractInverseRetractionMethod)Generate the inverse retraction with inverse retraction r to use in the embedding.
ManifoldsBase.EmbeddedRetraction — Type
EmbeddedRetraction{T<:AbstractRetractionMethod} <: AbstractRetractionMethodCompute a retraction by using the retraction of type T in the embedding and projecting the result.
Constructor
EmbeddedRetraction(r::AbstractRetractionMethod)Generate the retraction with retraction r to use in the embedding.
ManifoldsBase.ExponentialRetraction — Type
ExponentialRetraction <: AbstractRetractionMethodRetraction using the exponential map.
Though you would call e.g. retract(M, p, X, ExponentialRetraction()), to implement this retraction, define exp!(M, q, p, X) for your manifold M. The fused variant exp_fused!(M, q, p, X, t), which retracts t*X without forming that product, falls back to that and can additionally be implemented for performance reasons.
ManifoldsBase.InverseRetractionWithKeywords — Type
InverseRetractionWithKeywords{T<:AbstractInverseRetractionMethod,K} <: AbstractInverseRetractionMethodSince inverse retractions might have keywords, this type is a way to set them as an own type to be used as a specific inverse retraction. Another reason for this type is that we dispatch on the inverse retraction first and only the last layer would be implemented with keywords, so this way they can be passed down.
Fields
inverse_retractionthe inverse retraction that is decorated with keywordskwargsthe keyword arguments
Note that you can nest this type. Then the most outer specification of a keyword is used.
Constructor
InverseRetractionWithKeywords(m::T; kwargs...) where {T <: AbstractInverseRetractionMethod}Specify the subtype T <:AbstractInverseRetractionMethod to have keywords kwargs....
ManifoldsBase.LogarithmicInverseRetraction — Type
LogarithmicInverseRetraction <: AbstractInverseRetractionMethodInverse retraction using the logarithmic map.
ManifoldsBase.NLSolveInverseRetraction — Type
NLSolveInverseRetraction{T<:AbstractRetractionMethod,TV,TK} <:
ApproximateInverseRetractionAn inverse retraction method for approximating the inverse of a retraction using NLsolve.
Constructor
NLSolveInverseRetraction( method::AbstractRetractionMethod[, X0]; project_tangent=false, project_point=false, nlsolve_kwargs...,)Constructs an approximate inverse retraction for the retraction method with initial guess X0, defaulting to the zero vector. If project_tangent is true, then the tangent vector is projected before the retraction using project. If project_point is true, then the resulting point is projected after the retraction. nlsolve_kwargs are keyword arguments passed to NLsolve.nlsolve.
ManifoldsBase.PadeInverseRetraction — Type
PadeInverseRetraction{m} <: AbstractInverseRetractionMethodAn inverse retraction based on the Padé approximation of order $m$ for the retraction.
Though you would call e.g. inverse_retract(M, p, q, PadeInverseRetraction(m)), to implement an inverse Padé retraction, define inverse_retract_pade!(M, X, p, q, m) for your manifold M.
ManifoldsBase.PadeRetraction — Type
PadeRetraction{m} <: AbstractRetractionMethodA retraction based on the Padé approximation of order $m$
Constructor
PadeRetraction(m::Int)Though you would call e.g. retract(M, p, X, PadeRetraction(m)), to implement a Padé retraction, define retract_pade!(M, q, p, X, m; kwargs...) for your manifold M. The fused variant retract_pade_fused!(M, q, p, X, t, m; kwargs...), which retracts t*X without forming that product, falls back to that and can additionally be implemented for performance reasons.
ManifoldsBase.PolarInverseRetraction — Type
PolarInverseRetraction <: AbstractInverseRetractionMethodInverse retractions that are based on a singular value decomposition of the matrix / matrices for point and tangent vector on a AbstractManifold
Though you would call e.g. inverse_retract(M, p, q, PolarInverseRetraction()), to implement an inverse polar retraction, define inverse_retract_polar!(M, X, p, q) for your manifold M.
ManifoldsBase.PolarRetraction — Type
PolarRetraction <: AbstractRetractionMethodRetractions that are based on singular value decompositions of the matrix / matrices for point and tangent vectors.
Though you would call e.g. retract(M, p, X, PolarRetraction()), to implement a polar retraction, define retract_polar!(M, q, p, X; kwargs...) for your manifold M. The fused variant retract_polar_fused!(M, q, p, X, t; kwargs...), which retracts t*X without forming that product, falls back to that and can additionally be implemented for performance reasons.
ManifoldsBase.ProjectionInverseRetraction — Type
ProjectionInverseRetraction <: AbstractInverseRetractionMethodInverse retractions that are based on a projection (or its inversion).
Though you would call e.g. inverse_retract(M, p, q, ProjectionInverseRetraction()), to implement an inverse projection retraction, define inverse_retract_project!(M, X, p, q) for your manifold M.
ManifoldsBase.ProjectionRetraction — Type
ProjectionRetraction <: AbstractRetractionMethodRetractions that are based on projection and usually addition in the embedding.
Though you would call e.g. retract(M, p, X, ProjectionRetraction()), to implement a projection retraction, define retract_project!(M, q, p, X; kwargs...) for your manifold M. The fused variant retract_project_fused!(M, q, p, X, t; kwargs...), which retracts t*X without forming that product, falls back to that and can additionally be implemented for performance reasons.
ManifoldsBase.QRInverseRetraction — Type
QRInverseRetraction <: AbstractInverseRetractionMethodInverse retractions that are based on a QR decomposition of the matrix / matrices for point and tangent vector on a AbstractManifold
Though you would call e.g. inverse_retract(M, p, q, QRInverseRetraction()), to implement an inverse QR retraction, define inverse_retract_qr!(M, X, p, q) for your manifold M.
ManifoldsBase.QRRetraction — Type
QRRetraction <: AbstractRetractionMethodRetractions that are based on a QR decomposition of the matrix / matrices for point and tangent vector on a AbstractManifold
Though you would call e.g. retract(M, p, X, QRRetraction()), to implement a QR retraction, define retract_qr!(M, q, p, X; kwargs...) for your manifold M. The fused variant retract_qr_fused!(M, q, p, X, t; kwargs...), which retracts t*X without forming that product, falls back to that and can additionally be implemented for performance reasons.
ManifoldsBase.RetractionWithKeywords — Type
RetractionWithKeywords{R<:AbstractRetractionMethod,K} <: AbstractRetractionMethodSince retractions might have keywords, this type is a way to set them as an own type to be used as a specific retraction. Another reason for this type is that we dispatch on the retraction first and only the last layer would be implemented with keywords, so this way they can be passed down.
Fields
retractionthe retraction that is decorated with keywordskwargsthe keyword arguments
Note that you can nest this type. Then the most outer specification of a keyword is used.
Constructor
RetractionWithKeywords(m::T; kwargs...) where {T <: AbstractRetractionMethod}Specify the subtype T <:AbstractRetractionMethod to have keywords kwargs....
ManifoldsBase.SasakiRetraction — Type
struct SasakiRetraction <: AbstractRetractionMethod endExponential map on TangentBundle computed via Euler integration as described in [MF12]. The system of equations for $\gamma : ℝ \to T\mathcal M$ such that $γ(1) = \exp_{p,X}(X_M, X_F)$ and $γ(0)=(p, X)$ reads
\[\ddot{γ}(t) = (\ddot{p}(t), \ddot{X}(t)) = (R(X(t), \dot{X}(t))\dot{p}(t), 0)\]
where $R$ is the Riemann curvature tensor (see riemann_tensor).
Constructor
SasakiRetraction(L::Int)In this constructor L is the number of integration steps.
Though you would call e.g. retract(M, p, X, SasakiRetraction(L)), to implement this retraction, define retract_sasaki!(M, q, p, X, m; kwargs...) for your manifold M. The fused variant retract_sasaki_fused!(M, q, p, X, t, m; kwargs...), which retracts t*X without forming that product, falls back to that and can additionally be implemented for performance reasons.
ManifoldsBase.SoftmaxInverseRetraction — Type
SoftmaxInverseRetraction <: AbstractInverseRetractionMethodDescribes an inverse retraction that is based on the softmax function.
Though you would call e.g. inverse_retract(M, p, q, SoftmaxInverseRetraction()), to implement an inverse softmax retraction, define inverse_retract_softmax!(M, X, p, q) for your manifold M.
ManifoldsBase.SoftmaxRetraction — Type
SoftmaxRetraction <: AbstractRetractionMethodDescribes a retraction that is based on the softmax function.
Though you would call e.g. retract(M, p, X, SoftmaxRetraction()), to implement a softmax retraction, define retract_softmax!(M, q, p, X; kwargs...) for your manifold M. The fused variant retract_softmax_fused!(M, q, p, X, t; kwargs...), which retracts t*X without forming that product, falls back to that and can additionally be implemented for performance reasons.
ManifoldsBase.StabilizedInverseRetraction — Type
StabilizedInverseRetraction <: AbstractInverseRetractionMethodAn inverse retraction wraps another inverse retraction and projects the resulting tangent vector onto the corresponding tangent space for numerical stability.
Constructor
StabilizedInverseRetraction(::AbstractInverseRetractionMethod=LogarithmicInverseRetraction())See also
ManifoldsBase.StabilizedRetraction — Type
StabilizedRetraction <: AbstractRetractionMethodA retraction wraps another retraction and projects the resulting point onto the manifold for numerical stability.
Constructor
StabilizedRetraction(::AbstractRetractionMethod=ExponentialRetraction())See also
ManifoldsBase.ShootingInverseRetraction — Type
ShootingInverseRetraction <: ApproximateInverseRetractionApproximating the inverse of a retraction using the shooting method.
This implementation of the shooting method works by using another inverse retraction to form the first guess of the vector. This guess is updated by shooting the vector, guessing the vector pointing from the shooting result to the target point, and transporting this vector update back to the initial point on a discretized grid. This process is repeated until the norm of the vector update falls below a specified tolerance or the maximum number of iterations is reached.
Fields
retraction::AbstractRetractionMethod: The retraction whose inverse is approximated.initial_inverse_retraction::AbstractInverseRetractionMethod: The inverse retraction used to form the initial guess of the vector.vector_transport::AbstractVectorTransportMethod: The vector transport used to transport the initial guess of the vector.num_transport_points::Int: The number of discretization points used for vector transport in the shooting method. 2 is the minimum number of points, including just the endpoints.tolerance::Real: The tolerance for the shooting method.max_iterations::Int: The maximum number of iterations for the shooting method.
The functions on layer 3
While you should always add your documentation to retract or retract! when implementing new manifolds, the actual implementation happens on the following functions on layer III.
ManifoldsBase.inverse_retract_approx! — Method
inverse_retract_approx!(M::AbstractManifold, X, p, q, m::ApproximateLogarithmicInverseRetraction)Compute the in-place variant of the ApproximateLogarithmicInverseRetraction m.
ManifoldsBase.inverse_retract_cayley! — Method
inverse_retract_cayley!(M::AbstractManifold, X, p, q)Compute the in-place variant of the CayleyInverseRetraction, which by default calls the first order PadeInverseRetraction.
ManifoldsBase.inverse_retract_embedded! — Method
inverse_retract_embedded!(M::AbstractManifold, X, p, q, m::AbstractInverseRetractionMethod)Compute the in-place variant of the EmbeddedInverseRetraction using the AbstractInverseRetractionMethod m in the embedding (see get_embedding) and projecting the result back.
ManifoldsBase.inverse_retract_nlsolve! — Method
inverse_retract_nlsolve!(M::AbstractManifold, X, p, q, m::NLSolveInverseRetraction; kwargs...)Compute the in-place variant of the NLSolveInverseRetraction m.
ManifoldsBase.inverse_retract_pade! — Method
inverse_retract_pade!(M::AbstractManifold, X, p, q, m::PadeInverseRetraction)Compute the in-place variant of the PadeInverseRetraction m.
ManifoldsBase.inverse_retract_polar! — Method
inverse_retract_polar!(M::AbstractManifold, X, p, q; kwargs...)Compute the in-place variant of the PolarInverseRetraction.
ManifoldsBase.inverse_retract_project! — Method
inverse_retract_project!(M::AbstractManifold, X, p, q; kwargs...)Compute the in-place variant of the ProjectionInverseRetraction.
ManifoldsBase.inverse_retract_qr! — Method
inverse_retract_qr!(M::AbstractManifold, X, p, q; kwargs...)Compute the in-place variant of the QRInverseRetraction.
ManifoldsBase.inverse_retract_softmax! — Method
inverse_retract_softmax!(M::AbstractManifold, X, p, q; kwargs...)Compute the in-place variant of the SoftmaxInverseRetraction.
ManifoldsBase.retract_approx! — Method
retract_approx!(M::AbstractManifold, q, p, X, m::ApproximateExponentialRetraction)Compute the in-place variant of the ApproximateExponentialRetraction m.
ManifoldsBase.retract_cayley! — Method
retract_cayley!(M::AbstractManifold, q, p, X)Compute the in-place variant of the CayleyRetraction, which by default falls back to calling the first order PadeRetraction.
ManifoldsBase.retract_embedded! — Method
retract_embedded!(M::AbstractManifold, q, p, X, m::AbstractRetractionMethod)Compute the in-place variant of the EmbeddedRetraction using the AbstractRetractionMethod m in the embedding (see get_embedding) and projecting the result back.
ManifoldsBase.retract_embedded_fused! — Method
retract_embedded_fused!(M::AbstractManifold, q, p, X, t::Number, m::AbstractRetractionMethod)Compute the scaled variant of retract_embedded!.
ManifoldsBase.retract_fused — Function
retract_fused(M::AbstractManifold, p, X, t::Number, method::AbstractRetractionMethod=default_retraction_method(M, typeof(p)))
retract_fused!(M::AbstractManifold, q, p, X, t::Number, method::AbstractRetractionMethod=default_retraction_method(M, typeof(p)))A variant of retract that performs retraction on the vector X scaled by t. This can be faster in some cases compared to multiplying X by t, especially when performing this for multiple values of t. This can be computed in-place of q.
By default, this falls back to calling retract with t*X.
This fallback is happening on the in-place variant in Layer 3. Hence implementing this performant variant requires to implement the corresponding third layer fused function, like for example retract_polar_fused!. The “non-fused” variant always also has to be implemented, but can then be just specified to fallback to the fused variant. for example
retract_polar!(M, q, p, X) = retract_polar_fused!(M, q, p, X, one(eltype(p)))ManifoldsBase.retract_fused! — Function
retract_fused(M::AbstractManifold, p, X, t::Number, method::AbstractRetractionMethod=default_retraction_method(M, typeof(p)))
retract_fused!(M::AbstractManifold, q, p, X, t::Number, method::AbstractRetractionMethod=default_retraction_method(M, typeof(p)))A variant of retract that performs retraction on the vector X scaled by t. This can be faster in some cases compared to multiplying X by t, especially when performing this for multiple values of t. This can be computed in-place of q.
By default, this falls back to calling retract with t*X.
This fallback is happening on the in-place variant in Layer 3. Hence implementing this performant variant requires to implement the corresponding third layer fused function, like for example retract_polar_fused!. The “non-fused” variant always also has to be implemented, but can then be just specified to fallback to the fused variant. for example
retract_polar!(M, q, p, X) = retract_polar_fused!(M, q, p, X, one(eltype(p)))ManifoldsBase.retract_pade! — Method
retract_pade!(M::AbstractManifold, q, p, X, m::PadeRetraction; kwargs...)Compute the in-place variant of the PadeRetraction m.
ManifoldsBase.retract_pade_fused! — Method
retract_pade_fused!(M::AbstractManifold, q, p, X, t::Number, m::PadeRetraction; kwargs...)Compute the in-place variant of the PadeRetraction m of t*X.
ManifoldsBase.retract_polar! — Method
retract_polar!(M::AbstractManifold, q, p, X; kwargs...)Compute the in-place variant of the PolarRetraction.
ManifoldsBase.retract_polar_fused! — Method
retract_polar_fused!(M::AbstractManifold, q, p, X, t::Number; kwargs...)Compute the in-place variant of the PolarRetraction of t*X.
ManifoldsBase.retract_project! — Method
retract_project!(M::AbstractManifold, q, p, X; kwargs...)Compute the in-place variant of the ProjectionRetraction.
ManifoldsBase.retract_project_fused! — Method
retract_project_fused!(M::AbstractManifold, q, p, X, t::Number; kwargs...)Compute the in-place variant of the ProjectionRetraction of t*X.
ManifoldsBase.retract_qr! — Method
retract_qr!(M::AbstractManifold, q, p, X; kwargs...)Compute the in-place variant of the QRRetraction.
ManifoldsBase.retract_qr_fused! — Method
retract_qr_fused!(M::AbstractManifold, q, p, X, t::Number; kwargs...)Compute the in-place variant of the QRRetraction of t*X.
ManifoldsBase.retract_sasaki! — Method
retract_sasaki!(M::AbstractManifold, q, p, X, m::SasakiRetraction)Compute the in-place variant of the SasakiRetraction m.
ManifoldsBase.retract_sasaki_fused! — Method
retract_sasaki_fused!(M::AbstractManifold, q, p, X, t::Number, m::SasakiRetraction; kwargs...)Compute the in-place variant of the SasakiRetraction m of t*X.
ManifoldsBase.retract_softmax! — Method
retract_softmax!(M::AbstractManifold, q, p, X; kwargs...)Compute the in-place variant of the SoftmaxRetraction.
ManifoldsBase.retract_softmax_fused! — Method
retract_softmax_fused!(M::AbstractManifold, q, p, X, t::Number; kwargs...)Compute the in-place variant of the SoftmaxRetraction of t*X.
ManifoldsBase.inverse_retract_shooting! — Method
inverse_retract_shooting!(M::AbstractManifold, X, p, q, m::ShootingInverseRetraction)Approximate the inverse of a retraction using the shooting method.